C# ile Doğrusal Regresyon Kodlayalım

Daha önce K-Means demetleme algoritmasını C# ile beraber yazmıştık. Bu yazıda ise biraz daha kolay bir kod ile beraberiz. Yapacağımız işin en genel haline "regresyon analizi", "bağlanım çözümlemesi", "doğrusal bağlanım" gibi isimler verilmektedir. Peki nedir, ne işe yarar? Regresyon analizi verinin dağılımına uyan en uygun doğruyu bulmaya yarar. Bu doğruyu bulmak ne işimize yarayacak? Bu doğru sayesinde artık veri noktalarına ihtiyacımız kalmayacak çünkü herhangi bir durumu tanımlayacak denklemimiz olacak bu aradaki ve gelecekteki değerlerin ne olduğunu tahmin etme gücüne de kavuşturacak. Ama pek tabii verilerimizin doğrusal şekilde dağılması gerekiyor ki mümkün olduğunca güzel sonuçlar elde edelim. Örneğin bilinen bir konum için, hava sıcaklığı arttıkça limonata satışları artıyor ise bunun doğru denklemi olarak yazabiliriz. Ama dolar kuru, borsa, bitcoin değeri gibi daha kaotik şeylerde pek bir şey beklemeyin 🙂

Çalışmak için veri

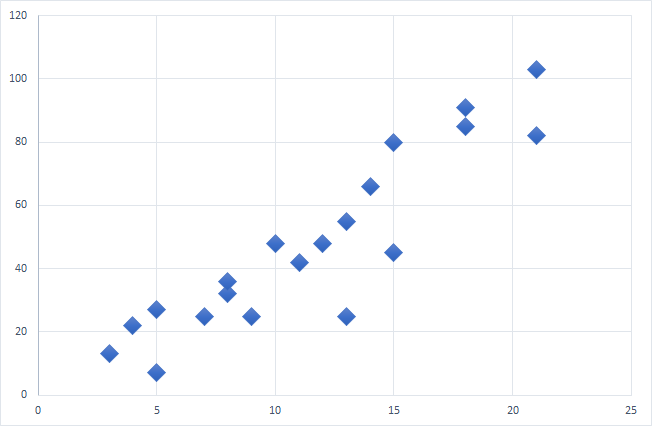
Çalışmak ve grafiğe dökebilmek için 2 boyutlu bir veriye ihtiyacımız olacak. Doğrusal regresyona uygun şöyle bir veri hazırladım.

    var xler = new[] { 13, 4, 12, 8, 7, 3, 8, 10, 9, 21, 11, 15, 18, 18, 15, 14, 5, 21, 5, 13 };
    var yler = new[] { 25, 22, 48, 32, 25, 13, 36, 48, 25, 82, 42, 80, 91, 85, 45, 66, 27, 103, 7, 55 };

Bunun grafiğini çıkarttığımızda ise sonuç şöyle oluyor:

Amaç

Amacımız bu veriyi ifade eden en uygun doğruyu bulmak. Bunu öncelikle Excel ile bulalım. Noktalardan birisine sağ tıklayıp "add a trendline" seçeneğini seçiyorum ve açılan ayar kutusundan "linear" yani "doğrusal" olanı seçiyorum. Türkçe Excel'de karşılığını öğrenince yazıyı düzenlerim :).

Bir kaç görsel değişiklik yapınca verimiz için oluşan doğru şu şekilde olacak:

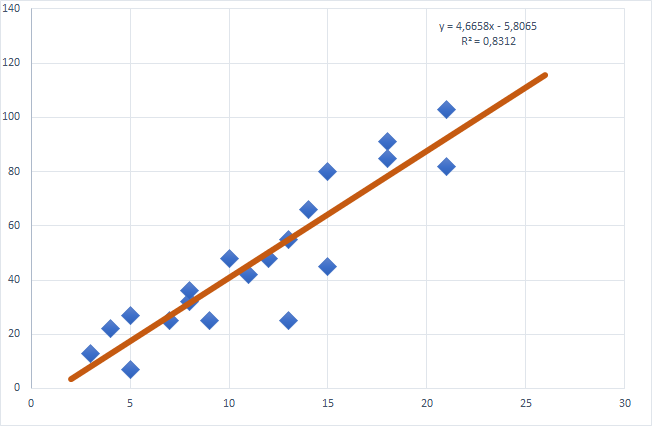
Örneğin ben artık bu noktaya bakarak X 25 olduğunda Y değerinin 110 civarında olacağını kestirebiliyorum.

İşin Matematiği

Bu yazıda LSM (en küçük kareler, least-squares regression line method) metodunu kullanacağız kendisini çözmek için çok basit bir eşitliğimiz var.

y = ((\frac{\sum{Y_i}}{n}) - ((\frac{n\sum({x_i}*{y_i}) - \sum{x_i}*\sum{y_i}}{\sqrt{n\sum{{x_i^2}}-(\sum{x_i})^2} *\sqrt{n\sum{{y_i^2}}-(\sum{y_i})^2} }) * \frac{\sqrt{\frac{\sum(X_i - \overline{X})^2}{n-1}}}{\sqrt{\frac{\sum(Y_i - \overline{Y})^2}{n-1}}}) * (\frac{\sum{X_i}}{n})) + ((\frac{n\sum({x_i}*{y_i}) - \sum{x_i}*\sum{y_i}}{\sqrt{n\sum{{x_i^2}}-(\sum{x_i})^2} *\sqrt{n\sum{{y_i^2}}-(\sum{y_i})^2} }) * \frac{\sqrt{\frac{\sum(X_i - \overline{X})^2}{n-1}}}{\sqrt{\frac{\sum(Y_i - \overline{Y})^2}{n-1}}})x

"Ağam bizimle eğleniyor" demeyin. Aşure gibi duran yığını biraz incelediğinizde aslında tekrarlayan bir çok kalıp olduğunu göreceksiniz ve şayet formülün geometri ile ilgili olduğunu fark ederseniz çözüm çorap söküğü gibi gelecek. En temelinde bu aslında bir doğru denkleminden başka bir şey değil. En yalın hali ile olay şu:

\hat{y}= a + bx

Formüldeki değerleri ise şu bağlantılardan bulacağız:

y = a + b * x
r = kovaryans / (YStdSapma * XStdSapma)
b = r * (YStdSapma / XStdSapm)
a = YOrtalama - b * XOrtalama

Bunu bir fonksiyon olarak ifade etmek istersek f(x)=a+bx diyebiliriz. adeğeri x 0 olduğunda y nin değeridir. b değeri ise doğrunun y eksenini kestiği yere göre nasıl döndüğünü vermektedir. a değeri arttıkça doğru yukarı doğru hareket ederken, b değeri yükseldikçe doğru dikleşecektir.
a değerindeki değişimin etkisi

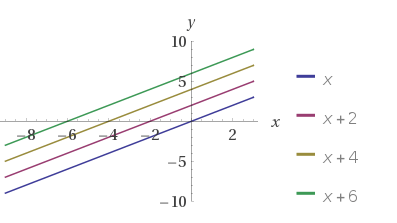
b değerindeki değişim etkisi:

Elimizdeki verilere bakarak a ve b değerlerini bulmamız gerekmektedir. b değerini bulabilmek için:

b=r*\frac{s_y}{s_x}

Formüldeki r değeri ise Pearson korelasyon kat sayısına denk geliyor. s değerleri ise ilgili dizilerin standart sapmalarıdır.

a değerini bulmak için ise aşağıdaki eşitliğin çözümüne ihtiyacım var.

a=\bar{y}-b\bar{x}

Üsteki formül ise ylerin ortalmasından x lerin ortalamasının b ile çarpılmış halini çıkartmamızı istiyor.

Elimizdeki veriler ile hesap makinesi yardımıyla bu değerleri bulalım ve her adımda ne yaptığımızı açıklayayım.

Öncelikli olarak bazı değerleri bulup kenera not almamız gerekecek.

X'lerin ortalaması
Y'lerin ortalaması
X'lerin standart sapması
Y'lerin standart sapması

Ortalama almak kolay, hepsini toplayıp eleman sayısına böleceğiz.

\mathcal{X ort.}~~ \frac{13+4+12+8+7+3+ \dots +5+21+5+13}{19} = 11.5
\\~\\
\mathcal{Y ort.}~~\frac{25+22+48+32+25+ \dots 103+7+55}{19} = 47.85

Standart sapma için ise örneklem standart sapmasını kullanacağız. Standart sapmanın ne olduğuna ve hesaplama detaylarına merkezi dağılım ölçülerini anlattığım yazıda değinmiştim.
Standart sapma için kullanacağımız formül

s = \sqrt{\frac{\sum(X_i - \overline{X})^2}{n-1}}

Anlamı her bir elemanı ortalamadan çıkart ve karesini al ve hepsini topla ardından eleman sayısının 1 eksiğine böl. Sonra çıkan sayının karekökünü al.

\mathcal{X s.sapma}~~ \sqrt{\frac {(13- 11.5)^2 + (4- 11.5)^2 + (12- 11.5)^2+ \dots +(13 - 11.5) ^2}{19}} \approx 5.4627
\\~\\
\mathcal{Y s.sapma}~~ \sqrt{\frac {(25- 47.85)^2 + (22- 47.85)^2 + (48- 47.85)^2 + (32- 47.85)^2 + \dots + (55- 47.85)^2}{19}} \approx 27.9572

Hesaplamanın devamında yardımcı olacak değişkenlerimizi bulduk.

\bar{X} = 11.5 \\
\bar{Y} = 47.85 \\
s_x \approx 5.4627 \\
s_y \approx 27.9572

Hesaplamaya r değerini bularak devam edelim. Daha önce Pearson Korelasyonunun nasıl hesaplanacağını ve ne olduğunu anlatmıştım. Özet geçmek gerekirse iki sayı dizisinden birindeki değişiklik diğer diziyi ne ölçüde etkiliyor onu bulmayı amaçlıyor. Eğer sonuç 1 veya -1 çıkarsa bu durumda verilen her x değeri için y değerinin kesin olarak bilineceği anlamı çıkmaktadır. Örneğin, kümelerimiz {1,2,3} ve {2,4,6} olsunlar. Bu durumda ilişki gücü 1 çıkacaktır. Zira ilk kümedeki tüm değerler için ikinci kümedeki değeri sadece 2 katını alarak bulabilmekteyiz. Kümelerin {1,2,3} ve {6,4,2} olduğu durumda ise ilişki ters yöndedir ve -1 çıkacaktır.

Pearson korelasyonu için iki örnek veya kitle için iki formül vardı örnek için olanı alacağız

r_{xy} = \frac{\sum{(x-\bar{x})(y-\bar{y})}}{\sqrt{\sum{(x-\bar{x})^2}}\sqrt{\sum{(y-\bar{y})^2}}}

ya da

r_{xy} = \frac{kovaryans(x,y)}{S_x * S_y}

Demiştik, kovaryans ise

\sum_{i=1}^N{\frac{(x_i - \bar{x})(y_i - \bar{y})}{N-1}}

ile bulunuyordu. Bu durumda n-1 li ifadeyi aşağı yazmamda sıkıntı olmayacaktır.

r_{xy} = \frac{\sum{(x-\bar{x})(y-\bar{y})}}
{s_x * s_y * (n-1)}

ve r değerini aşağıdaki gibi hesaplamış oluruz:

r_{xy} = \frac{2645.5}{5.4627 * 27.9572 * 19} \approx 0.9117

r değerini bulduğumuza göre b değerini bulabiliriz.

b = r * \frac{s_y}{s_x} = 0.9117 * \frac{27.9572}{5.4627} \approx 4,666

Çorap söküğü gibi geliyor, bu durumda a değeri ise:

a = \bar{y} - b\bar{x} =  47.85 - 4,666 * 11.5 \approx -5.807

Bu durumda doğru denklemimiz ortaya çıkacaktır:

y = -5.8065 + 4.6658x

Bulduğumuz bu sayıları Excel'de benzer yollardan geçerek bulmuştu. Şimdi sıra bu matematiği C#'a dökmekte. Yukarıda konuştuğumuz kadar kod çıkmayacak 🙂

public static Func<double, double> RegresyonModeliOlustur(double[] dizi1, double[] dizi2)
{
    var uzunluk = dizi1.Length;
    if (uzunluk != dizi2.Length)
    {
        throw new Exception("Uzunluklar Aynı Olmalı");
    }

    var xOrtalama = dizi1.Average();
    var yOrtalama = dizi2.Average();

    var xKareUzakliklarToplami = 0D;
    var yKareUzakliklarToplami = 0D;
    var xyUzakliklarCarpimiToplami = 0D;

    for (int i = 0; i < uzunluk; i++)
    {
        var x = dizi1[i];
        var y = dizi2[i];

        var xUzaklik = xOrtalama - x;
        var yUzaklik = yOrtalama - y;

        xKareUzakliklarToplami += Math.Pow(xUzaklik, 2);
        yKareUzakliklarToplami += Math.Pow(yUzaklik, 2);
        xyUzakliklarCarpimiToplami += xUzaklik * yUzaklik;
    }

    var xStandartSapma = Math.Sqrt(xKareUzakliklarToplami / (uzunluk - 1D));
    var yStandartSapma = Math.Sqrt(yKareUzakliklarToplami / (uzunluk - 1D));
    var kovaryans = xyUzakliklarCarpimiToplami / (uzunluk - 1D);

    var r = (kovaryans / (xStandartSapma * yStandartSapma));
    var b = r * (yStandartSapma / xStandartSapma);
    var a = yOrtalama - b * xOrtalama;

    // f(x) = a + bx;
    var parametre = Expression.Parameter(typeof(double), "x"); // x'i tanımla
    var ifade = Expression.Lambda(Expression.Add(Expression.Constant(a), // a +
                                  Expression.Multiply(Expression.Constant(b), // b *
                                                      parametre) // x
                                                      ),
                                 parametre);// (x) =>

    return ifade.Compile() as Func<double, double>;
}

Kod sırasıyla yukarıda yaptığımız işlemleri yapmakta. En sonda ise çalışma zamanında bir metot oluşturuyoruz. Expression kütphanesi Linq'in de canını oluşturuyor. Bu kütüphane ile C# ifadelerini kod ile oluşturabiliyoruz. Bu fonksiyonda son kısımda oluşan doğru denklemini bir C# metodu olarak geriye dönüyor. Delegate kullanımına da güzel bir örnek bence:) Kullanımı ise şu şekilde olacak:

    var xs = new double[] { 13, 04, 12, 08, 07, 03, 08, 10, 09, 21, 11, 15, 18, 18, 15, 14, 05, 21, 05, 13 };
    var ys = new double[] { 25, 22, 48, 32, 25, 13, 36, 48, 25, 82, 42, 80, 91, 85, 45, 66, 27, 103, 07, 55 };

    var model = RegresyonModeliOlustur(xs, ys);
    Console.WriteLine("13 =>" + model(13)); //54.8
    Console.WriteLine("21 =>" + model(21)); //92.1

Peki bu model ne güvenilir? Excel grafiğinde bir R2 değeri göreceksiniz. Bu doğrunun anlatım gücünü temsil ediyor. Kendisinin formülü ve kodunu ise şöyle:

{SS}_{top} =  \sum_{i}{(y_i - \bar{y})^2} \\
{SS}_{res} =  \sum_{i}{(f_i - y_i)^2} \\
~\\
R^2 \equiv 1 - \frac{{SS}_{res}}{{SS}_{top}}

public static double R2(double[] dizi1, double[] dizi2,  Func<double, double> model)
{
    var yOrtalama = dizi2.Average();
    var SS_toplam = dizi2.Sum(y => Math.Pow(y - yOrtalama, 2));
    var SS_artik = dizi1.Select((x, i) => Math.Pow(model(x) - dizi2[i], 2)).Sum();
    return (1.0 - SS_artik / SS_toplam);
}

Bunu örnek veriye uyguladığımızda 0.83 değerini alıyoruz bu da bize %83 oranında doğru sonuç alacağımızı söylüyor.

Peki ama birden fazla bağımsız değişken varsa ne yapacağız? Girişte verdiğim eşitliğin aslında açık hali şu şekilde:

\hat{y} \approx \beta_0 + \beta_1x_ + \beta_2x_2+\beta_3x_3...

olan formülün tek bağımsız değişken için yazılmış haliydi. O da başka bir yazının konusu olsun.

Ekstra kaynaklar:
İşin biraz daha derinliklerine inmek istiyorsanız http://www.veridefteri.com 'a mutlaka bakın derim.

Başka algoritmalarda görüşmek üzere.