Doğrusal regresyonun (doğrusal bağlanım) ne olduğundan ve çözüm yöntemlerinden birisi olan en küçük kareler yönteminin (LSM) C# ile nasıl kodlanacağından bir önceki yazıda bahsetmiştim. İnce detaylar için sizi o yazıya alalım 🙂 Doğrusal regresyon verilen değerleri sağlayan en uygun doğru denklemini bulmayı amaçlıyordu. İşin matematiğine girmeden ne yaptığımızı biraz açıklayayım.
Aşağıdaki grafiği inceleyin.
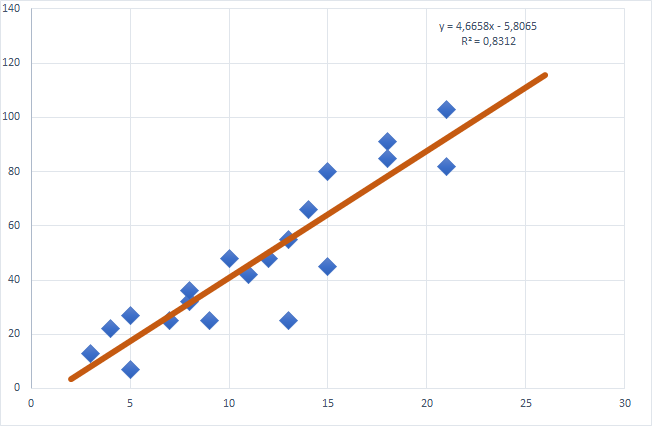
Mavi veri noktalarının dağılımına uygun doğrulardan birisi turuncu olarak hesaplanmış ve grafikte gösterilmiştir. Buradan hareketle X eksenindeki herhangi bir değerin Y eksenindeki karşılığı bulunabilmektedir. Bunu, gerçek Dünyadan örneklemek istersek, sıcaklığa göre satış miktarı, tecrübeye göre maaş miktarı, yüzey alanına göre ev fiyatı gibi hesaplamalarda değerlerden birinin artışı veya azalışı diğer nitelikte her zaman aynı veya zıt yönde değer alıyorsa, (hemen her zaman sıcaklık arttıkça dondurma satışları artıyorsa gibi) bunu bir doğru denklemi ifade edebiliriz. Uygun doğrunun tespiti için farklı yöntemler bulunmaktadır. Ama genel olarak amaç mevcut noktaların doğruya olan uzaklıklarının toplamının en küçük olduğu doğruyu bulmaktadır.
Önce veri
Tüm örneklerde olduğu gibi bu hesaplamayı da yapabilmek için veriye ihtiyacımız olacak. Kaggle üzerinden şöyle kısa bir örneğimiz var: https://www.kaggle.com/kennethjohn/linear-regression-from-scratch/data
Örneğin sayfasında kademeli azaltma ile çözümde mevcut. İnceleyin derim.
2104,3,399900
1600,3,329900
2400,3,369000
1416,2,232000
3000,4,539900
1985,4,299900
1534,3,314900
1427,3,198999
1380,3,212000
1494,3,242500
1940,4,239999
2000,3,347000
1890,3,329999
4478,5,699900
1268,3,259900
2300,4,449900
1320,2,299900
1236,3,199900
2609,4,499998
3031,4,599000
1767,3,252900
1888,2,255000
1604,3,242900
1962,4,259900
3890,3,573900
1100,3,249900
1458,3,464500
2526,3,469000
2200,3,475000
2637,3,299900
1839,2,349900
1000,1,169900
2040,4,314900
3137,3,579900
1811,4,285900
1437,3,249900
1239,3,229900
2132,4,345000
4215,4,549000
2162,4,287000
1664,2,368500
2238,3,329900
2567,4,314000
1200,3,299000
852,2,179900
1852,4,299900
1203,3,239500Studio
Azure ML Studio'ya oldukça alıştığınızı tahmin ediyorum. Bu sebeple, tuvale atıp birbirine bağlayacağımız kutuları komple gösteriyorum. Sonra sırasıyla neyi neden yaptığımızdan ve sonuçlarından bahsedeceğim.
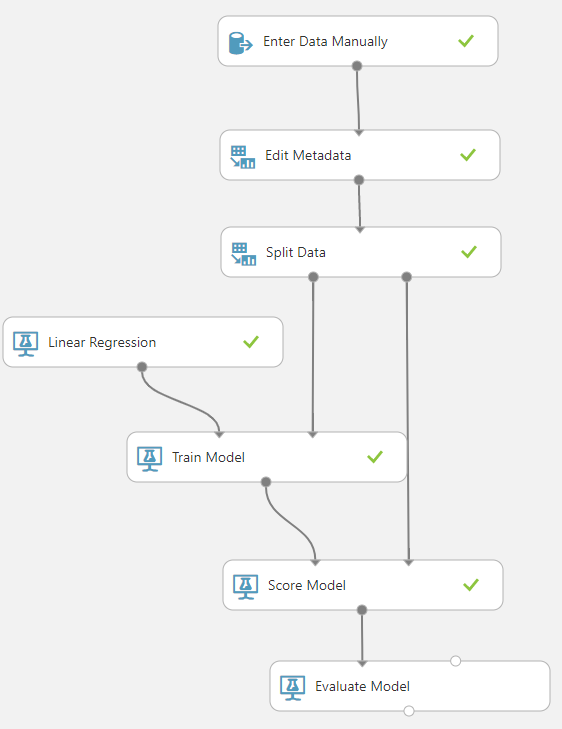
Enter Data Manually
Bu kutucuğa yukarıdaki verimizi kopyala yapıştır yöntemiyle veriyoruz. Başlık satırları olmadığını belirtmeyi unutmuyoruz aksi halde ilk satırdaki verileri kaybederiz.
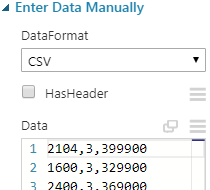
Edit Metadata
Verimizde başlık satırları yok. Bu daha sonra neyin ne olduğunu anlamamızı zorlaştırabilir. Sorunu çözmek için bu kutucuk yardımıyla hangi kolonun ne anlama geldiğini ekliyoruz. Launch Colum Selector ile tüm kolonları sağa taşıdıktan sonra yapmamız gerekenler resimde mevcut:
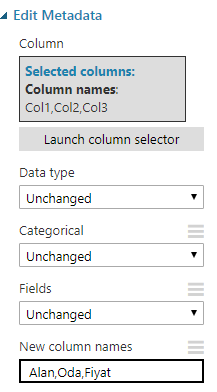
Her şey doğru ise sonucu görselleştirdiğimizde kolonları adlarıyla görüyor olmalıyız.
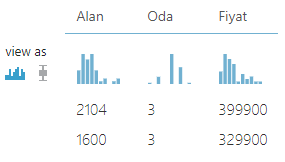
Split Data
Yaptığımız şey bir yerde makine öğrenmesi ve biz bunu test etmeliyiz. Öğrenme işlemi gerçekleştirdikten sonra, daha önce öğrenme için kullanmadığımız noktalar ile başarımı tekrar ölçerek bu işlemi yapacağız. %70 (öğretim) -%30 (test) ayırma bu iş için yeterli olacaktır. Kullanacağımız veri için bu 33 adet öğrenme 14 adet test verisi içeren ayırma işlemi demek.
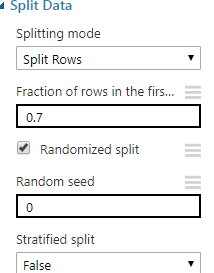
Train Model
Train model kutucuğu Azure ML studioda gözetimli öğrenme işlemlerinde kullanılıyor. Bağımlı değişkeni yani sonucuyla ilgilendiğimiz değeri "Launch column selecto" ile seçiyoruz. Bu veri için diğer değişkenlerin değerine göre "Fiyat" değişkenini bulmak istediğimizden bağımlı değişkenimiz kendisidir.
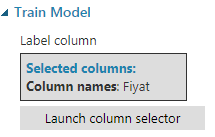
Linear Regression
Doğrusal regresyon veya doğrusal bağlanım için farklı hesaplama yöntemleri olduğundan bir önceki yazıda bahsetmiştim. Azure ML Studio da bunları içeriyor.
Solution Method
Ordinary Least Squares (en düşük kareler metodu) bizim bir önceki yazıda kullandığımız formüle denk gelmektedir. Fakat yaptığımız hesapta yalnızca bir tane bağımsız değişken vardı. Tek bağımsız değişken olan duruma basit bağlanım (simple regression) adı verilirken, bu örneğimizdeki gibi birden fazla bağımsız değişken olan durumlara çok değişkenli doğrusal bağlanım (multivariate linear regression) denilmektedir. Azure ML Studio çok değişkenli olarak hesaplama yapabilmektedir.
Online Gradient Descent, kademeli azaltma yöntemi doğruyu oluşturan katsayıların en düşük sonucu verecek yönde kademe kademe değiştirilmesi ile sonucu bulmaya çalışmaktadır. Kademelerin büyüklüğünü learning rate parametresi belirlemektedir. Epochs algoritmanın kaç tur döneceğini belirmektedir. Özellikle az veri olan durumlarda yüksek bir değer girmenizde fayda var. L2 regularization weight ya da diğer adıyla "Ridge Regularization" fazla öğrenmeden kaçınmadan için maliyet fonksiyonuna eklenen bir değerin ağırlığını belirtir. "Normalize features" niteliklerin 0 ile 1 arasında normalleştirilmesini sağlamaktadır. "Decrease learning rate" öğrenme çarpanını döngülerde azaltarak başlangıçta büyük adımlar sonrasında daha küçük adımlar atmayı sağlar.
Score Model
İkiye ayırdığımız verinin test için olanını bu kutuya bağlıyoruz. Bu modülde test verisinin sonuna bir kolon daha ekleyip modele göre değerini eklemektedir.
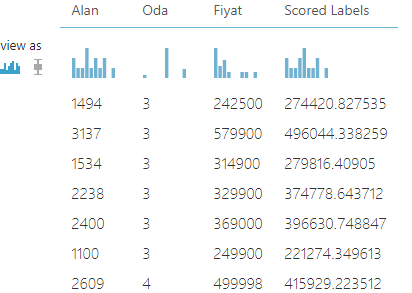
Evaluate Model
Score model en sağa modelin tahminini yazmıştı. Bu veride aynı zamanda gerçekte olması gereken değerde var. Bu ikisinden ne kadar başarılı bir modelimiz olduğunu tek tek kendimizde hesaplarız ama büyük verilerde külfetli olacaktır. Bu kutucuk bunu bizim için yapıyor. Önceki yazılarda da detaylarına girdiğim için kendi yaptığım çalışmadaki sonucu paylaşıyorum.
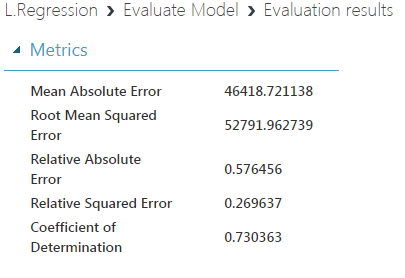
Ben LSM'ye göre sonuç aldım. Sayıların anlamları ise aşağıdaki gibi:
| Metrik | Değer | Açıklama |
|---|---|---|
| Mean Absolute Error | 46418 | Gerçek değer ile tahmin değerlerinin mutlak değerlerinin ortalaması |
| Root Mean Squared Error | 52791 | Gerçek değer ile tahmin değerlerinin kareli farklarının ortalamasının karekökü |
| Relative Absolute Error | 0.576456 | MAE nın gerçek değerlerin ortalamadan farkına bölümü |
| Relative Squared Error | 0.269637 | RMS nin gerçek değerlerin ortalamadan farkına bölümü |
| Coefficient of Determination | 0.730363 | Oransal olarak, tahminin gerçeği ne kadar yansıttığını gösterir. R² kare değeri olarak da gösterilir. |
Başka bir yazıda görüşmek üzere.


