Kaldığımız yerden CNTK'ye merhaba dediğimiz projemize devam ediyoruz. Bir önceki yazıda CNTK için gerekli kurulumları yaptık, veriyi temin ettik ve ağ modelimizi oluşturduk. Bu yazıda ise öğretme işlemine, modelin oluşturulmasına ve doğrulanması konularına bakıyor olacağız.
Kaldığımız yere aşağıdaki kodu ekleyerek devam ediyoruz.
var etiketler = CNTKLib.InputVariable(new[] { etiketAdedi }, DataType.Float);
var maliyetFonksiyonu = CNTKLib.CrossEntropyWithSoftmax(new Variable(siniflandiriciCiktisi), etiketler, "maaliyetFonksiyonu");
var tahmin = CNTKLib.ClassificationError(new Variable(siniflandiriciCiktisi), etiketler, "siniflandirmaHatasi");İlk satırda önce boş bir değişken (variable) oluşturuyoruz. Bu değişken her bir rakam için olasılıkları tutacak.
Maliyet (cost) veya kayıp (loss) fonksiyonu modelin tahmin ettiği sınıfın olması gerekten sınıftan ne kadar uzaklaştığını ölçen fonksiyonlara denilmektedir. Bu satırda maliyet fonksiyonu olarak "Cross Entropy" kullanılırken öncesinde "SoftMax" fonksiyonu çalıştırılmaktadır.
Softmax
Model girdinin hangi rakama benzediğini bulurken aşağıdakine benzer bir girdi çıktı durumu yaşanır.
0 => 0.314750449878513
1 => 0.0611163197369856
2 => 0.0970889805336897
3 => 0.894234456072671
4 => 0.197270659262906
5 => 0.162531984673129
6 => 0.0429778022891738
7 => 0.39371517747348
8 => 0.0281869053971893
9 => 0.196992759498299Her bir rakam için farklı olasılıklar üretilir ve tahmin edilirken bunun en yüksek değerlisi kabul edilir. Bu karar verme süreci için yeterlidir ama değerlendirme sürecinde biraz daha iş gerekmektedir. Çünkü gerçekte olması gerekenden ne kadar uzakta bir tahmin yapıldığını bilmemiz gerekir. Yukarıdaki örnekte tahminin 3 rakamı yönünde olduğunu söyleriz. Fakat rakamların genelinde kaç olasılıkla 3 dür? Burada naif düşünürsek her bir değeri, değerler toplamına bölebiliriz. Fakat bu durumda, çıktı sayısı arttıkça ve bir birine yakın değerlerde problem yaşarız. Detaylara ayrıca bir yazıda değinmek isterim ama konunun dışına çıkmak istemiyorum. SoftMax yukarıdaki çıktıyı aşağıdaki gibi toplamları 1 olacak şekilde olasılık dağılımına (logaritmik) çevirecektir.
0 => 0.31 => 0.10
1 => 0.06 => 0.08
2 => 0.10 => 0.08
3 => 0.89 => 0.19
4 => 0.20 => 0.09
5 => 0.16 => 0.09
6 => 0.04 => 0.08
7 => 0.39 => 0.11
8 => 0.03 => 0.08
9 => 0.20 => 0.09Böylece aslında 3 için %19 olasılık verildiğini söyleyebiliriz. Bu da doğru bilinse de epey bir kötü tahmin yapıldığını gösterir.
Merak edenler için Softmax'ın formülü ise
P_i = \frac{exp({x_i})}{\sum{exp({x})}}
Cross Entropy
👻 Entropi ile ilgili yazıma davetlisiniz.
Eğitim verimizde hangi resmin hangi rakama ait olduğunun bilgisi vardı. Bir tahmin yaptık ve olasılık dağılımını biliyoruz. Seçeceğimiz öğrenme algoritmasının da modelin ürettiği sonuca bakıp model içindeki parametreleri düzenlemesi gerekmekte. Peki ama modelin ürettiği sonuç gerçek sonuca ne kadar benziyor? %19 çıktığına göre %81 uzaklıkta diyebilir miyiz? Aslında demek mümkün. Fakat yakın değerlerde daha küçük uzak değerlerde çok daha büyük adımlar atmak daha doğru olacaktır. Yapacağımız işlem modelin entropi hesabını gerçek sonucun entropi sonucuna göre yapmak ve aradaki farkı almak olacak. Şunun gibi düşünün X dosyasını sıkıştırmak için bir anahtar ürettim ve Y dosyasını sıkıştırırken aynı anahtarı kullanıyorum. Haliyle Y dosyası yeterince iyi sıkışmayacaktır. En fazla X'in sıkıştığı kadar sıkışabilir ki bu durumda X ve Y bir birine eşittir. Bu konuyu daha sonra uzunca yazmayı düşündüğümden direkt formülü veriyorum.
D(T,G) = -\sum_{i}{G_i \ln(T_i)}Burada T tahmin edilen değeri, G ise gerçek değeri temsil ediyor. Softmax örneğimiz için hesabı yapalım.
Bu formül çoklu sınıflandırma için aynı zamanda "Negative Log likelihood" formülüne denk gelmektedir.
-(0 * ln(0.10) = 0 +
0 * ln(0.08) = 0 +
0 * ln(0.08) = 0 +
1 * ln(0.19) = -1.68200759672924 +
0 * ln(0.09) = 0 +
0 * ln(0.09) = 0 +
0 * ln(0.08) = 0 +
0 * ln(0.11) = 0 +
0 * ln(0.08) = 0 +
0 * ln(0.09) = 0 )
= 1.68Gerçek veride yalnızca 3 için 1 değeri varken diğer sınıflar için 0 değeri vardı. Dolayısıyla onlar hesaba dahil edilmediler. Şayet 0.19 dan daha yüksek bir değer çıksaydı sayı giderek 0 yaklaşacak ve 1 olduğunda 0 sonucuna ulaşacaktı. Burada 2 tabanı yerine e tabanının seçilmesinin bir çok sebebi olsa da en temel sebebi türev alma işinin daha kolay olması. Yoksa herhangi bir tabanda benzer şekilde iş görecektir. Maksat 1'de 0 değerine ulaşmak.
Koda devam
var miniBatchKaynağı = MinibatchSource.TextFormatMinibatchSource(
Path.Combine(ImageDataFolder, "train.cntk.txt"), akisAyarlari,
MinibatchSource.InfinitelyRepeat);
var nitelikAkisBilgisi = miniBatchKaynağı.StreamInfo(nitelikAkisAdi);
var etiketAkisBilgisi = miniBatchKaynağı.StreamInfo(etiketAkisAdi);
var ogrenmeOrani = new TrainingParameterScheduleDouble(0.004111, 1);
IList<Learner> ogrenmeParametreleri = new List<Learner>
{Learner.SGDLearner(siniflandiriciCiktisi.Parameters(), ogrenmeOrani)};
var ogretici = Trainer.CreateTrainer(siniflandiriciCiktisi, maliyetFonksiyonu, tahmin, ogrenmeParametreleri);
Burada en can alıcı kısım Trainer.CreateTrainer bu metod bir öğretici oluşturuyor. Öğreticiye öncelikle modelin çıktısını, ardından maliyet fonksiyonumuzu veriyoruz. Tahmin kısmı değerlendirme fonksiyonunu alıyor. Parametreler ise öğrenme algoritması ve öğrenme değerini içeriyor. SGD (stochastic gradient descent) en bilindik algoritmalardan bir tanesi. Öğrenme değeri ise parametreler düzenlenirken adımların büyüklüğü için kullanılıyor. Öğrenme değeri başarılı bir algoritma için doğru değeri bulana kadar epey uğraşmamız gereken bir değer.
Gelelim dananın kuyruğuna. Öğrenme işlemi için kodumuz aşağıdaki gibi.
const uint miniBatchBoyutu = 100;
var i = 0;
var epochs = 20;
while (epochs > 0)
{
var minibatchData = miniBatchKaynağı.GetNextMinibatch(miniBatchBoyutu, cihaz);
var arguments = new Dictionary<Variable, MinibatchData>
{
{girdi, minibatchData[nitelikAkisBilgisi]},
{etiketler, minibatchData[etiketAkisBilgisi]}
};
ogretici.TrainMinibatch(arguments, cihaz);
if (++i % 100 == 0)
{
var trainLossValue = ogretici.PreviousMinibatchLossAverage();
Console.WriteLine($"E: {21 - epochs} M: {i} CrossEntropyLoss = {trainLossValue * 100000,0:0}");
}
if (minibatchData.Values.Any(a => a.sweepEnd))
{
--epochs;
}
}
Eğitim dosyamızda 60000 adet resim bulunuyor. Bunu 100'lük parçalara bölüyoruz. Eğitim 100erlik parçalar haline yapacak. Epoch ise eğitim verisinin üzerinden kaç kere dolaşacağımızı belirtiyor. TrainMinibatch metodu parçayı kullanarak ağın parametrelerini düzenliyor.
Her 100 minibatch'de ekrana eğitim durumunu basıyoruz. "CrossEntropyLoss" değeri son batch içindeki tüm resimler için tahmin edilen değerin gerçek değerden uzaklığının ortalamasını içeriyor. Ekranı ondalıklı sayıların bilimsel gösterimi ile doldurmamak için büyük bir sayı ile çarpmayı tercih ettim. Ayrıca değişkenler koyup epoch içindeki ortalamayı da bulmak mümkün tabii.
Çalıştırdığımız da çıktımız aşağıdaki gibi olacaktır.
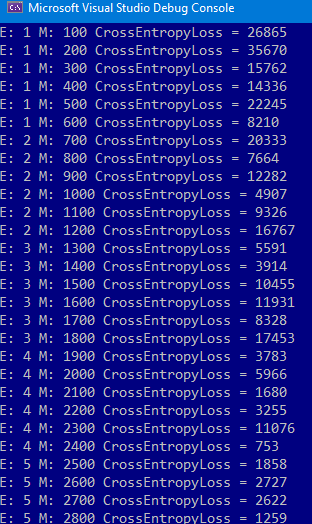
Arada düzensizlikler olsa da giderek ağımızın kendisini eğitim verisine uydurduğunu ve ortalama uzaklığın düştüğünü görebiliyoruz.
Bizim bir de içindeki hiç bir resmi eğitim sırasında kullanmadığımız 10000 adet test verimiz vardı. Bu veri ile de oluşturduğumuz modelin ne kadar başarılı olduğunu göreceğiz.
Öncelikle modeli kaydedelim.
siniflandiriciCiktisi.Save(modelDosyasi);Modelimiz sürücümüze kaydedildi. Artık herhangi bir projede verilen resmin hangi rakama ait olduğunu söyleyebilir.
Bu aşamada grafik kartınızın kullanılıp kullanılmadığını görmek isteyebilirsiniz. Bunu iki basit yolla anlamak mümkün. Birincisi, cihaz değişkenine GPU değil de CPU değerini atayın. Örneği çalıştırdığınızda satırların bariz daha yavaş geldiğini göreceksiniz. İkincisi ise gizli katmanlardan birisine 100000 gibi bir değer verin ve görev yöneticisi ni açın. GPU sekmesinde kıpırdanmalar olacaktır.
[========]
Doğrulama işlemi
Önce kod konuşsun.
var batchBoyutu = 1000;
int toplamHataliTahminAdedi = 0, toplamResimAdedi = 0;
while (true)
{
var minibatchData = testMinibatchSource.GetNextMinibatch((uint) batchBoyutu, cihaz);
if (minibatchData == null || minibatchData.Count == 0) break;
toplamResimAdedi += (int) minibatchData[testNitelikAkisBilgisi].numberOfSamples;
var etiketVerisi = minibatchData[etiketAkisBilgisi].data.GetDenseData<float>(etiketCiktisi);
var beklenenEtiketler = etiketVerisi.Select(l => l.IndexOf(l.Max())).ToList();
var girdiEslemesi = new Dictionary<Variable, Value>
{
{resimGirdisi, minibatchData[testNitelikAkisBilgisi].data}
};
var ciktiEslemesi = new Dictionary<Variable, Value>
{
{etiketCiktisi, null}
};
model.Evaluate(girdiEslemesi, ciktiEslemesi, cihaz);
var ciktiBilgisi = ciktiEslemesi[etiketCiktisi].GetDenseData<float>(etiketCiktisi);
var tahminEdilenEtiketler = ciktiBilgisi.Select(l => l.IndexOf(l.Max())).ToList();
var hatalar = tahminEdilenEtiketler.Zip(beklenenEtiketler, (a, b) => a.Equals(b) ? 0 : 1).Sum();
toplamHataliTahminAdedi += hatalar;
Console.WriteLine(
$"Örnek Sayısı = {toplamResimAdedi}, Hatalı Sınıflandırma = {toplamHataliTahminAdedi}");
}
var errorRate = 100.0F * toplamHataliTahminAdedi / toplamResimAdedi;
Console.WriteLine($"Model Hata Oranı = %{errorRate,0:0.00}");
BatchBoyutu test dosyasından satırları kaçar kaçar okuyacağımızı belirtiyor.
Ardından gelen iki değişken hata oranını hesaplayabilmek için döngünün dışına konuşlanmış durumda.
Sonsuz bir döngü başlatıyoruz, döngü miniBatch artık dosyadan satır çekemediğinde sona erecek.
Okunan parçadan etiket verilerini bir float dizisine alıyoruz.
Modele vermek ve modelin yanıtını almak için iki adet dictionary oluşturuyoruz.
En can alıcı kısım Evaluate metoduna geldik. Bu verdiğimiz girdiden bir çıktı üretiyor.
Cikti bilgisi sonucu float[][]'a çeviriyoruz. Her bir satır için hangi sınıfa ne kadar uyduğunun bilgisi yer alıyor.
tahminEdilenEtiketler dizisinde bir önceki dizide en yüksek değere sahip olan satırın indisini alıyoruz.
Hatalar kısmında tahminEdilenEtiketlerve beklenenEtiketler dizilerinin elemanlarını sırayla karşılaştırıyoruz. Aynı sıradaki elemanlar eşitse 0 değilse 1 dönüp topluyoruz. Böylece bu batch için hatalı tahmin adedini bulmuş oluyoruz.
Yekünü yazıp döngüye devam ediyoruz.
En sonunda genel hata oranını ekrana basıyoruz.
Ben parametreler ile çok fazla oynamadan %2.8 hata oranına ulaşabildim. Fakat gerçek kullanımda rakamlar hep aynı boyutta ve konumda olmayacaktır. Hatta eğri büğrü bile olabilirler. Burada devreye evrişimli ağlar giriyor. İlerleyen yazılarda bu konuya da eğilmek istiyorum.
Gelecek yazılarda görüşmek üzere.


