K-Means Algoritmasını C# ile baştan yazalım

K-Means Nedir ?

Makine öğrenmesi ile tanışma faslında ilk öğrenilen ve öğretilen algoritmaların başında K-Means algoritması gelmektedir. Neden? Çünkü, anlaması da anlatması da kolaydır. Kendisi bir demetleme algoritmasıdır. Her demetleme algoritması gibi verinin içinden anlamlı n adet grup oluşturmasını istersiniz ve yapar. Bu yazıda bu algoritmanın ne olduğuna bakacağız ve C# ile sıfırdan yazacağız. Fakat C# kısmında klasik takılmak yerine Linq, TPL, Tuple gibi .net yeteneklerini kullanıyor olacağım ve her satırda ne yaptığımızı açıklıyor olacağım. Bir iki ufak not ile başlayalım.

👉Clustering teriminin Türkçe karşılığı olarak demetleme, kümeleme, öbekleme, topaklama gibi kelimeler kullanılmaktadır. Ben alışkanlıktan dolayı "demetleme"yi kullanıyor olacağım.

👉 K-Means algoritması için K-Ortalamalar karşılığını görebilirsiniz.

🌊 K-Medoids, K-Median gibi farklı ama özü aynı olan algoritmalar veya K-Means++ gibi K-Means varyasyonları görebilirsiniz. Ama hepsinde önce bu yazıdaki en sade halini bilmekte fayda var.

🧔 Kendisini literatürde "Lloyd’s algorithm" olarak görebilirsiniz.

Çalışmak için veri üretelim

Algoritmayı adım adım anlatarak yazacağım için bu algoritmaya uygun temiz güzel bir veri lazım olacaktı, bunun için bir üreteç yazmak daha cazip geldi ve şöyle bir kod çıktı ortaya:

var random = new Random(55555); // seed değerini aynı tutarsanız siz de birebir aynı sayıları üreteceksiniz.
    var veri = Enumerable
                .Range(0, 30)
                .Select(n => n > 10
                                ? (x: random.Next(1, 06), y: random.Next(1, 06))
                                : (x: random.Next(6, 11), y: random.Next(6, 11))
                        )
                .OrderBy(_=>random.NextDouble())
                .ToList();

⚠ Kodda gördüğünüz (x:...,y:...) şeklinde olan kısım yabancı geldiyse Tuple kavramını anlamanız için sizi şöyle alalım: http://http://www.cihanyakar.com/c-7-0-ve-7-1-yenilikleri/

Enumerable.Range metodu bize ilk parametrede belirttiğimiz sayıdan itibaren ikinci parametredeki sayı kadar üretim yapıyor. Yani 0 dan başlayarak 30 adet sayı üretiyor.

Ardından gelen Selectmetodu içinde bu sayı 10 dan büyük ise x ve y niteliği için 1 ile 6 arasında rastgele sayı üretmesini; 10 veya küçük ise 6 ile 11 arasında iki sayı üretmesini istiyorum. Peki neden? Çünkü üreteceğim veriyi düzleme yerleştirdiğimde 2 ada şeklinde görülmesini istiyorum.

Peşinden OrderBy ile bu sayıların karışık şekilde üretilmesini sağlıyoruz.

Bu kod ile ürettiğim veriyi 2 boyutlu bir düzleme Excel yardımı ile geçirdiğimde manzara şöyle oluyor:

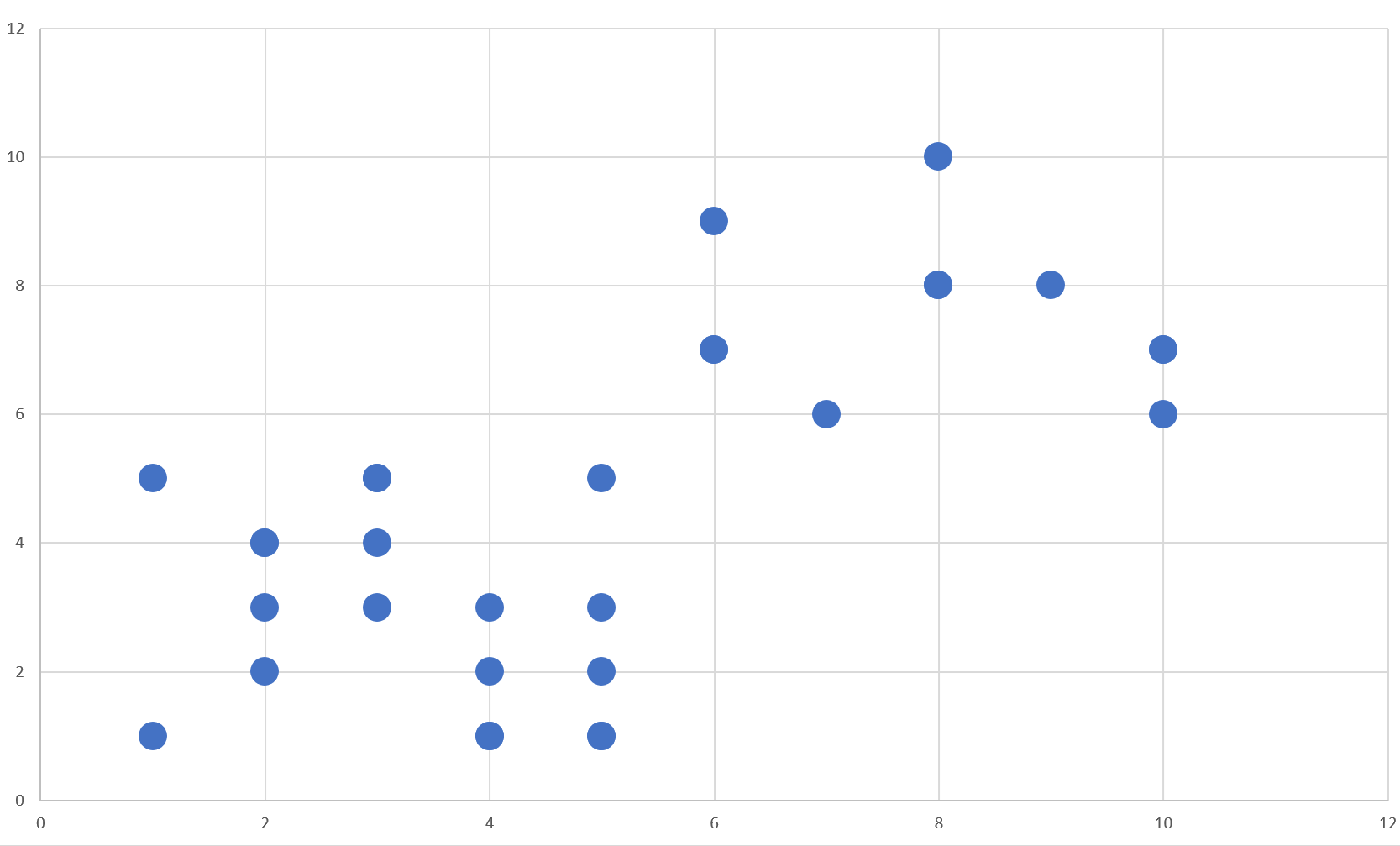
2 boyutlu klasik bir veri ürettik. Veriyi kafanızda daha somut hale getirmek adına niteliklerin ne olduğunu uydurabilirsiniz. Varsayalım ki yataydaki değerleri eğitim seviyesi, düşeydeki değerleri yılda ziyaret edilen müze sayısı olsun ne dediğimizin hiç bir önemi yok. Ama her iki niteliğin de değer aralığının aynı olmasına dikkat etmek gerekiyor. Örneğin, bir eksende "ağırlık", diğerinde "yıllık gelir" olursa değer aralıkları farklılaşacak ve algoritmamız yanlış sonuç üretecektir.

👉 Niteliklerin değer aralıkları farklılaştığında yapabileceğimiz çözümlerden birisi olan normalleştirme kavramına ML.net ve Normalizasyon yazımda değinmiştim.

Algoritmayı falan boş verip bu resimdeki noktaları 2 gruba ayırmam istenilse benim için cevap aşağıdaki gibi olacaktır:

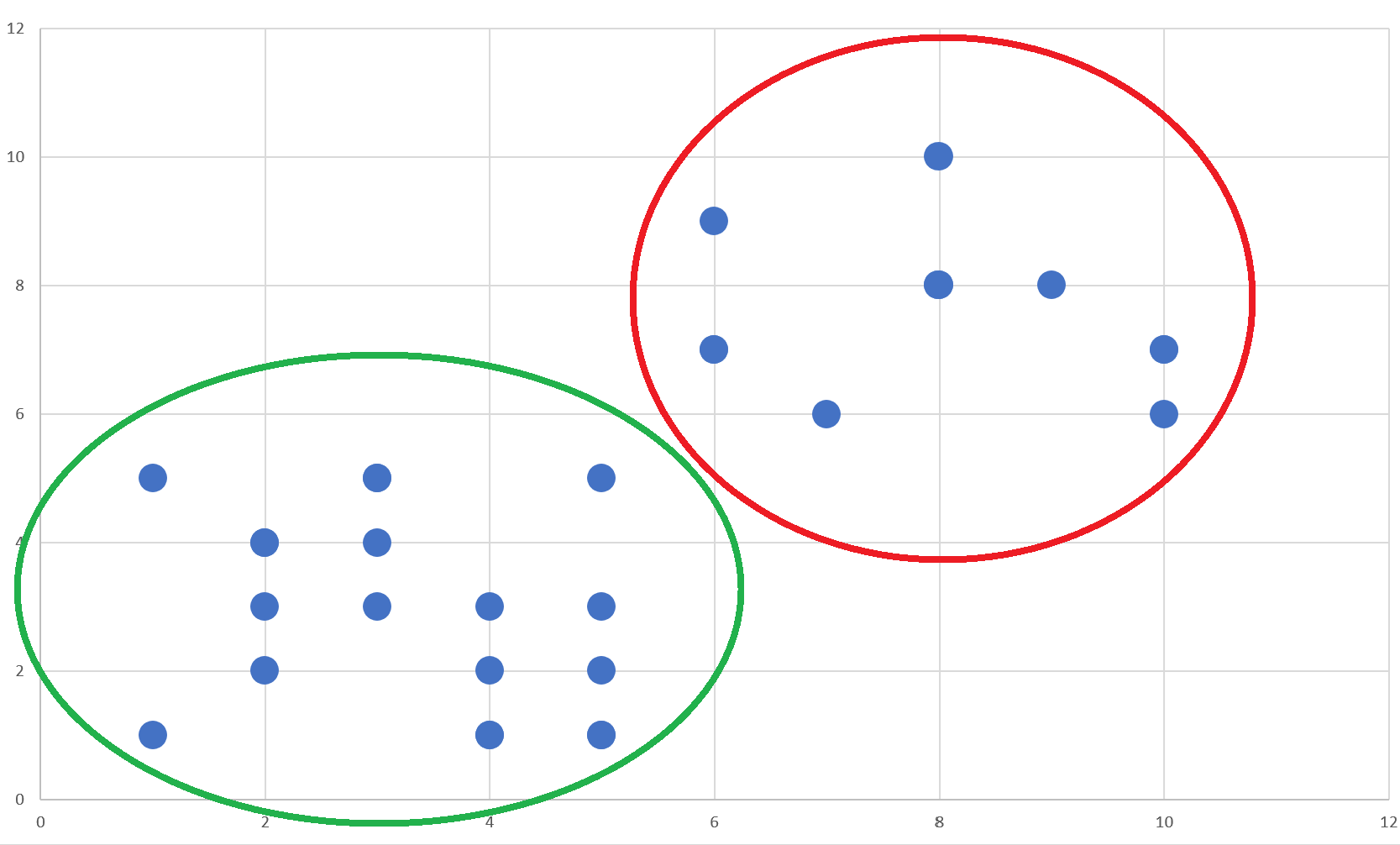
Çoğunuz da benzer düşünecektir diye umuyorum. İşte K-Means buradaki örüntüyü bizim için fark edecek. Peki ama nasıl?

Sözde kod

Yapacağımız işlemin adımları için sözde kodumuzu yazalım

Her bir satırı rastgele kümeye ata.

dönmeye başla
    Her grubun merkez noktasını bul
    Her bir satırın merkez noktaya olan uzaklığına bak
    Her bir satırın grubunu merkez noktası en yakın olan ile güncelle

    Grup güncellemesi yapılmadıysa döngüden çık
    Limite ulaşıldıysa döngüden çık
döngüden çık

Atanan değerleri dön

Adım adım nasıl yaptığımıza grafik üzerinden bakalım;

En başta sadece noktalarımız var:

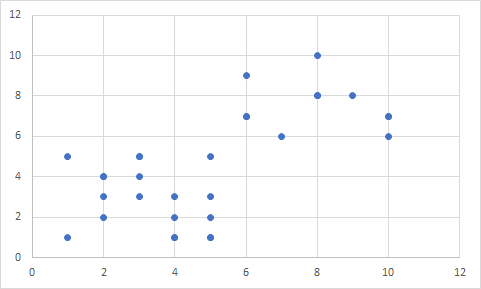
İki gruba rastgele atama yapıyoruz, (henüz merkezleri belirlemedik):

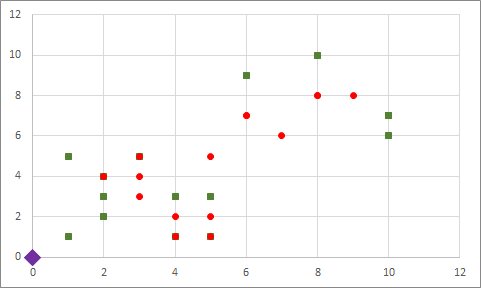
Rastgele atamaya göre merkezleri buluyoruz, yeşillerin merkezi için mor, kırmızıların merkezi için mavi şekli kullandım:

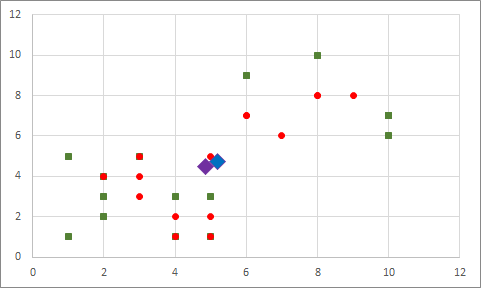
Merkez noktalara yakınlıklarına göre noktaların kümelerini değiştiriyoruz:

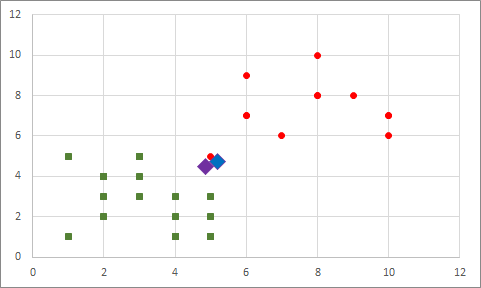
Ardından, yeni merkez noktalar hesaplıyoruz:

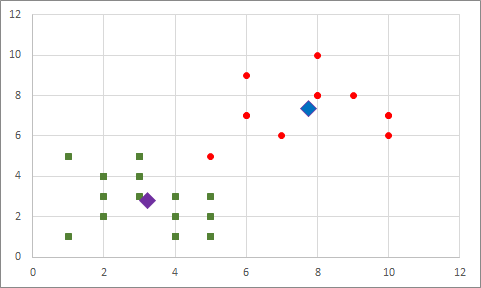
Tekrar en yakındakilere göre aktif kümeleri değiştiriyoruz:

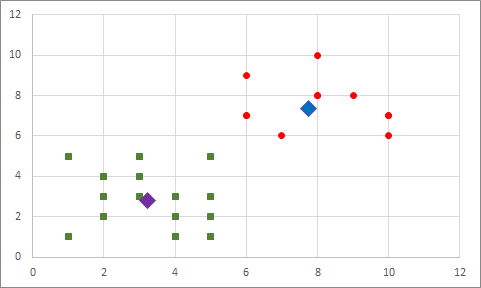
Atanmış kümesi değişen bir nokta olduğundan tekrar merkez noktaları hesaplıyoruz:

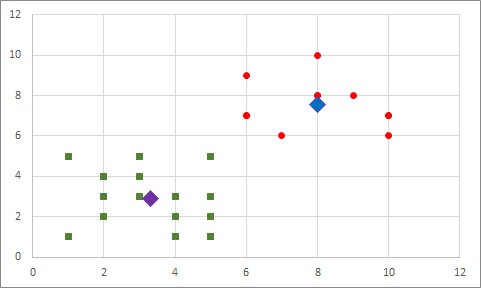
Bu merkez noktalar ile tekrar tek tek tüm elemanlara baktığımızda bir değişiklik gerekmiyor ve döngü sona eriyor. Artık elimizdeki veriler 2 farklı gruba atanmış oldu. Benim gözle yaptığım ayırmada yaptığımı oldukça yakın bir sonuç elde ettik.

Metodu yazmaya başlayalım

İlk ihtiyacımız olan tabi ki boş bir metot olacaktır. Kendisini aşağıdaki gibi oluşturuyorum:

static IList<int>[] KOrtalamalar(double[][] veri, int kumeSayisi){

    return null;
}

Metodumuzun dönüş değeri bir int dizisi, kendisine veri olarak gelen her bir satırın hangi gruba ait olduğunu dönecek. Örneğin yanit[0] değeri 1 ise, veri girdisinin ilk satırı 1. gruptandır anlamına geliyor olacak.

Metodun ilk girdisi veriyi temsil ediyor, burada sayısal değerler için oldukça geniş aralığa sahip olan double değerini tercih ettim. Jagged array formunda olmasının sebebi ise gelen verinin herhangi bir boyuttaki dizi olabilecek olması, böylece bu metodu istediğiniz herhangi bir veri seti ile kullanabilirsiniz.

Küme sayısı ise algoritmanın gelen veriyi kaça ayıracağını bildiriyor.

Bu metodun örnek verimiz ile kullanımı ise şu şekilde olacak:

    var diziFormu = veri.Select(n => new double[] { n.x, n.y }) // her bir satır için double dizi dön
                    .ToArray(); // double dizilerinden bir dizi oluştur

    var sonuc = KOrtalamalar(diziFormu, 2);

Adım 1 İlk Değer Ataması

Kaç gruba ayırmamız gerekiyorsa elimizdeki noktaları bu gruplara rastgele dağıtarak başlıyoruz. Algoritmanın rastgele olmayan varyasyonları mevcut biz sade takılacağız.

Metodumuzun içine aşağıdaki satırları yazarak başlıyoruz:

    var random = new Random(5555);
    // Her satırı rastgele bir kümeye ata
    var sonucKumesi = Enumerable
                            .Range(0, veri.Length)
                            .Select(index => (AtananKume: random.Next(0, kumeSayisi),
                                          Degerler: veri[index]))
                            .ToList();

İlk satırda rastgele sayı üreticini hazırlıyoruz, benimle aynı sayıları üretebilmeniz için bir seed değeri verdim kendisine.Bunu ayrıca metoda parametre olarak almanız daha faydalı olacaktır.

Ardından gelen satırda ise Range ile kaç satır verimiz varsa o kadar sayı üretiyoruz.
Select metodunda her bir satır için iki değerli bir Tuple oluşturuyoruz.

Bu tuple'a ilk olarak rastgele bir küme numarası atıyoruz.

Ardından da ilgili satırın verisini Degerler olarak saklıyoruz.

ToList() ile sorguyu çalıştırıp belleğe alıyoruz.

Bu işlemin ardından elimdeki veri kırmızılar 0. grup yeşiller 1.grup olmak şu şekilde rastgele sınıflanmış oluyor:

Bundan sonraki aşamada ana döngümüzü kuracağız. Öncesinde 3 değişken tanımlıyoruz:

    var boyutSayisi = veri[0].Length;
    var limit = 10_000;
    var guncellendiMi = true;

Boyut sayısını kod tekrarını azaltmak adına bir değişkene alıyoruz. Limit ise algoritmanın eşik değerini oluşturuyor, olur da 10.000 defa dönerse "yeter artık 😠" deyip kodu olduğu kadarıyla sonlandıracağız. Dilerseniz sayı değil zaman kısıtı da koyabilirsiniz; keyif sizin, mutfağınızda yazılımcı sizsiniz :). guncellendiMi değeri ise döngüyü sonlandıracak asıl değişkenimiz. Daha iyi bir demetleme yapamadığımız anda bu değişkenin değeri false olacak ve işlemi sonlandıracağız.

Döngümüzün ilk kısmında küme merkezlerini buluyor olacağız,

    while (--limit > 0)
    {
        // kümelerin merkez noktalarını hesapla
        var merkezNoktalar = Enumerable.Range(0, kumeSayisi)
                                        .AsParallel()
                                        .Select(kumeNumarasi =>
                                        (
                                        kume: kumeNumarasi,
                                        merkezNokta: Enumerable.Range(0, boyutSayisi)
                                                                            .Select(eksen => sonucKumesi.Where(s => s.AtananKume == kumeNumarasi)
                                                                            .Average(s => s.Degerler[eksen])) // 👇 AŞAĞIDA NOT VAR! 👇
                                                                            .ToArray())
                                                ).ToArray();

        // Sonuç kümesini merkeze en yakın ile güncelle
        guncellendiMi = false;
        // ...devam edecek...

Döngümüz eşik değeri 0'a eşit olana kadar devam edecek şekilde ayarladıktan sonra merkezi bulacak kısıma geçiyoruz.

Rangeile arzu edilen küme sayısı kadar sayı üretiyoruz.

AsParallel ise ardından gelecek döngünün multi thread çalışmasını sağlıyor olacak.

Select metodunda ise her küme için merkez noktayı hesaplıyoruz.

☝️ Kodun içinde ufak bir not var. Sebebi ise şu, eğer olur da bir kümeye hiç eleman düşmez ise ilgili satırda patlama yaşayabilirsiniz. Bu durum pek yaşanmaz ve orijinal algoritmada da ele alınmamıştır. Yine de duruma karşı çözüme gitmek isterseniz bir çok alternatif var. Küme sayısını azaltmak ilk akla gelendir fakat 4 küme istenip 2 küme ile döndüğünüzde bu hoş karşılanmayabilir. Bir diğeri ise başlangıç noktalarını tekrar seçmektir, fakat burada da yeniden deneme limiti koyulması gerekir. Bir diğeri ise doğrudan hata fırlatmaktır. Ben kodu gereksiz yere kalabalıklaştırmamak için böyle fevkalade bir durum oluşursa patlayacak şekilde bıraktım. Siz kendi uygulamalarınızda bu önerileri, literatürdeki diğer önerileri veya aklınıza gelen bambaşka bir fikri deneyebilirsiniz.

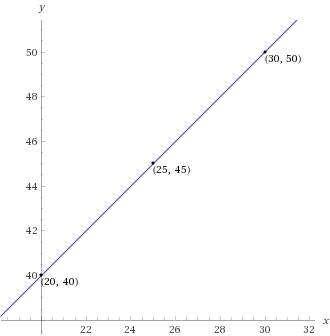
Merkez noktanın hesabında yine Rangeden yararlanarak verideki boyut sayısı kadar sayı oluşturuyoruz ardından ilgili kümeye atanmış verilerin ilgili eksenindeki değerlerin ortalamasını alıyoruz. Örneğin (20,40) ve (30,50) şeklinde iki noktamız olduğunda (20 + 30, 40 + 50) => (50 / 2, 90 / 2) => (25,45) olarak ortalamış oluyoruz.

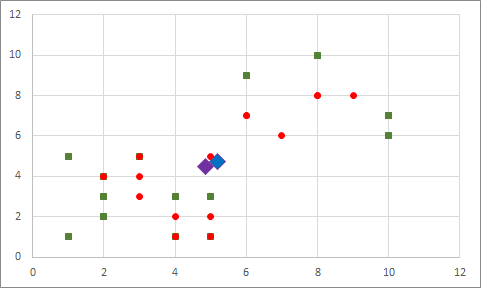
Bu işlemi yaptığımızda örnek verimiz için ilk döngüde orta noktalar (5.2 , 4.73) ve (4.86 , 4.46) olarak hesaplanacak. Düzlem üzerinde göstermek istersek aşağıdaki gibi sonucumuz olacaktır:

Sıradaki adımda her bir noktayı teker teker dolaşıp bu merkez noktalardan hangisine daha yakında bulunuyorsa ona göre atandıkları grubu değiştireceğiz. Burada pek tabii uzaklığı hesaplayacak bir fonksiyona ihtiyacımız olacak. Keyif yine sizin ama ben yine kolaya kaçıp öklid uzaklığını kullanacağım. Bunu hesaplamak için gereken formül ve formüle denk yazacağımız fonksiyon aşağıda.

İki boyut için uzaklık:

\sqrt {(x_1 - x_2)^2 + (y_1 - y_2)^2)}

Aslında bu formülü tanıyorsunuz, dik üçgende Pisagor teoremi vardı hatırlarsınız, kenarların ölçüsü ile hipotenüsü buluyorduk. Alın bu dik üçgeni kısa kenarlarının kesişim noktasını orijine koyun karşınız da Öklid uzaklığını göreceksiniz.

Gerçek hayatta verimiz 2 boyuttan oluşmuyor bu sebeple daha genel bir formüle ihtiyacımız var, N boyut için uzaklık:

\sqrt{\sum_{i=1}^{n}{(q_i - p_i)^2}}

N boyut için C# kodumuz:

static double UzaklikHesapla(double[] birinciNokta, double[] ikinciNokta)
{
    var kareliUzaklik = birinciNokta
                            .Zip(ikinciNokta,
                                (n1, n2) => Math.Pow(n1 - n2, 2)).Sum();
    return Math.Sqrt(kareliUzaklik);
}

Bu fonksiyon iki adet n elemanlı vektör alıyor.

Zip metodu iki adet dizinin sırayla elemanlarını dönen bir Linq metodudur. Örnek vermek gerekirse "cihan" ve "yakar" diye eşit sayıda elemanı olan dizi için sırasıyla (c,y),(i,a),(h,k)... şeklinde değer çiftleri olarak dönüş yapacaktır. Biz burada ilk vektörün ve ikinci vektörün her bir eksendeki değerlerini sırasıyla alıyoruz bir birilerinden çıkartıp sonucun karesini alıyoruz. Daha sonra tüm bu kareleri alınmış farkların genel bir toplamını alıyoruz.

Sonuç kısmında ise bu kareli toplamın karekökünü dönüyoruz. Örnekle ifade etmek gerekirse (20,40) ve (30,50) noktaları arasındaki mesafeyi ölçmek isteyelim. Bu durumda (20-30 , 40 - 50) => (-10,-10) => (100,100) => 200 => 10√2 => ~14 birim mesafe olduğunu söyleriz. Daha detaylı bilgi için tıklayın.

Dilerseniz, uzaklık hesabının son aşamasında karekök işlemini atlayabilirsiniz.

Uzaklık işini aradan çıkardığımıza göre döngümüze geri dönebiliriz. En yakın merkez noktaya göre yeniden atama yapacak kodumuz aşağıdaki gibi olacak:

        guncellendiMi = false;
        //for (int i = 0; i < sonucKumesi.Count; i++)
        Parallel.For(0, sonucKumesi.Count, i =>
                 {
                     var satir = sonucKumesi[i];
                     var eskiAtananKume = satir.AtananKume;

                     var yeniAtananKume = merkezNoktalar.Select(n => (KumeNumarasi: n.kume,
                                                                     Uzaklik: UzaklikHesapla(satir.Degerler, n.merkezNokta)))
                                          .OrderBy(x => x.Uzaklik)
                                          .First()
                                          .KumeNumarasi;

                     if (yeniAtananKume != eskiAtananKume)
                     {
                         sonucKumesi[i] = (AtananKume: yeniAtananKume, Degerler: satir.Degerler);
                         guncellendiMi = true;
                     }
                 });

        if (!guncellendiMi)
        {
            break;
        }
    } // while

Kodumuz Parallel.For ile başlamakta, kendisine eş olan klasik for döngüsünü açıklama olarak tepesine yazdım. Bunu tercih etmemin sebebi adı üzerinde kendisinin multi thread olarak çalışmasından kaynaklanıyor. Bu sayede işlemciyi daha verimli kullanan bir döngümüz olmuş oluyor. Kaç thread kullanılacağına kendisi karar veriyor vs. bizi bir çok dertten kurtarıyor. Parallel.For un ilk parametresi başlangıç değerini, ikinci parametresi ise bitiş değerini oluşturuyor.Üçüncü parametre ise tek bir int argümanı olan dönüşü void olan bir delegate beklemektedir. Delege işini inline method (lambda) olduğu yerde vererek başlıyoruz, bu satır içi metodun i değeri 0 dan başlayıp eleman sayımıza kadar artacak.

Döngünün içinde satır değişkeni mevcut veriyi tutmakta görevinde. Peşinden gelen eskiAtananKume ise bu satır için atanan bir önceki kümeyi tutuyor.

Yeni atanacak kümenin tespitinde her bir merkez noktayı tek tek dönüyoruz ve satir değerine olan uzaklığını ölçüyoruz. Sonra bu ölçümleri sıralayıp en düşüğünün küme numarasını dönüyoruz.

Yeni atanacak küme, eskisi ile aynı değilse o zaman sonuç kümemizde ilgili satırı güncelliyoruz ve güncellenen en az 1 veri olduğu için guncellendiMi değerini true konumuna çekerek bayrak kaldırıyoruz ve döngü sona eriyor.

Eğer guncellendiMi bayrağı havada değil ise yani false değerinde ise bu durumda hiç bir güncelleme olmamış demektir bu da büyük döngüyü sonlandırabileceğimiz anlamına geliyor.

Kodun tamamı ise şöyle:

static IList<int> KOrtalamalar(double[][] veri, int kumeSayisi)
{
    var random = new Random(5555);
    // Her satırı rastgele bir kümeye ata
    var sonucKumesi = Enumerable
                            .Range(0, veri.Length)
                            .Select(index => (AtananKume: random.Next(0, kumeSayisi),
                                          Degerler: veri[index]))
                            .ToList();

    var boyutSayisi = veri[0].Length;
    var limit = 10000;
    var guncellendiMi = true;
    while (--limit > 0)
    {
        // kümelerin merkez noktalarını hesapla
        var merkezNoktalar = Enumerable.Range(0, kumeSayisi)
                                        .AsParallel()
                                        .Select(kumeNumarasi =>
                                        (
                                        kume: kumeNumarasi,
                                        merkezNokta: Enumerable.Range(0, boyutSayisi)
                                                                            .Select(eksen => sonucKumesi.Where(s => s.AtananKume == kumeNumarasi)
                                                                            .Average(s => s.Degerler[eksen])) 
                                                                            .ToArray())
                                                ).ToArray();
        // Sonuç kümesini merkeze en yakın ile güncelle
        guncellendiMi = false;
        //for (int i = 0; i < sonucKumesi.Count; i++)
        Parallel.For(0, sonucKumesi.Count, i =>
                 {
                     var satir = sonucKumesi[i];
                     var eskiAtananKume = satir.AtananKume;

                     var yeniAtananKume = merkezNoktalar.Select(n => (KumeNumarasi: n.kume,
                                                                     Uzaklik: UzaklikHesapla(satir.Degerler, n.merkezNokta)))
                                          .OrderBy(x => x.Uzaklik)
                                          .First()
                                          .KumeNumarasi;

                     if (yeniAtananKume != eskiAtananKume)
                     {
                         sonucKumesi[i] = (AtananKume: yeniAtananKume, Degerler: satir.Degerler);
                         guncellendiMi = true;
                     }
                 });

        if (!guncellendiMi)
        {
            break;
        }
    } // while

    return sonucKumesi.Select(k => k.AtananKume).ToArray();
}

static double UzaklikHesapla(double[] birinciNokta, double[] ikinciNokta)
{
    var kareliUzaklik = birinciNokta
                            .Zip(ikinciNokta,
                                (n1, n2) => Math.Pow(n1 - n2, 2)).Sum();
    return Math.Sqrt(kareliUzaklik);
}

K-Means güzel bir algoritma fakat kullanılacak verinin çok fazla nitelik içermemesi ve dağılımın iç içe olmaması gerekiyor. Örneğin K-Means'in başarısz olduğu şu görsele bir bakın:

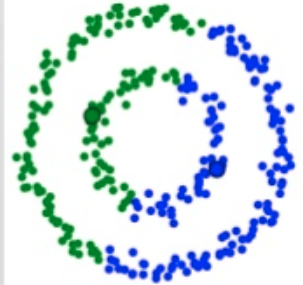
Bu gibi verilerle nasıl başa çıkacağımız da başka demetleyiciler başka yazıların konusu olsun.

Başka algoritmalarda, başka yazılarda görüşmek üzere.